Wir haben uns kürzlich mit dem Bitcoin Fear and Greed Index und seiner Vorhersagekraft beschäftigt. Es gibt jedoch auch andere Stimmungsindikatoren, für die solch eine Analyse naheliegend wäre. Einer davon ist der Colin Talks Crypto Bitcoin Bullrun Index (CBBI). Wir haben die gleiche Analyse, die wir für den Bitcoin Fear and Greed Index durchgeführt haben, auf den CBBI angewandt, um eine Vorstellung von dessen Zusammenhang mit zukünftigen Bitcoin-Entwicklungen zu bekommen.
Der CBBI ist interessant, weil er mehrere bekannte Unterindikatoren zu einer „Konfidenz“ kombiniert, dass der Bitcoin-Kurs einen Höchststand erreicht hat. Die offensichtliche Hypothese wäre also, dass hohe CBBI-Werte Verkaufsgelegenheiten anzeigen, während niedrige CBBI-Werte Kaufgelegenheiten anzeigen. Dies ist identisch mit den Erwartungen der meisten Menschen in Bezug auf den Bitcoin Fear and Greed Index oder eigentlich die meisten anderen Stimmungsindikatoren.
Die Unterindizes, aus denen sich der CBBI (im Juli 2022) zusammensetzt, sind die folgenden:
- Pi Cycle Top Indikator
- RUPL / NUPL Grafik
- RHODL-Verhältnis
- Puell-Multiplikator
- gleitender 2-Jahres-Durchschnitt
- Bitcoin Trololo Trendlinie
- MVRV Z-Score
- Reserve-Risiko
- Woobull Top Cap vs. CVDD
- Suchbegriff „Bitcoin“ (Google)
Die CBBI-Seite verweist auf die oben genannten Teilindizes, wo Einzelheiten zu diesen Indikatoren zu finden sind.
Letztendlich kombiniert der CBBI die Teilindikatoren so, dass die „Konfidenz“ zwischen 0 und 1 schwankt.
Daten für den Bitcoin Bullrun Index (CBBI) herunterladen
Glücklicherweise können die Daten für den CBBI in tabellarischer Form auf der CBBI-Website angezeigt werden, so dass sie gescrapet oder einfach nach Libre Office kopiert werden können. Die Tabelle enthält bereits den Bitcoin-Kurs sowie die Werte der Unterindikatoren, so dass wir alle Daten haben, die wir für diese Analyse benötigen. Es gibt auch eine API zum Abrufen der gleichen Daten.
library(tidyverse)
library(lubridate)
library(tidylog)
cbbi <- read_delim("CBBI-2022-05-07.csv", delim = ";")
cbbi <- cbbi %>%
mutate(
Date = mdy(Date),
Price = str_replace(string = Price, pattern = "\\$", replacement = ""),
Price = str_replace(string = Price, pattern = ",", replacement = ""),
Price = as.numeric(Price),
Confidence = str_replace(string = Confidence, pattern = "\\%", replacement = ""),
Confidence = as.numeric(Confidence)
) %>%
select(Date, Price, Confidence)
ggplot(cbbi, aes(x = Date, y = Confidence)) +
geom_point() +
scale_y_continuous(breaks = scales::pretty_breaks(n = 20)) +
geom_line() +
theme_bw(base_size = 15) +
ylab("") +
xlab("") +
ggtitle("CBBI")Code-Sprache: JavaScript (javascript)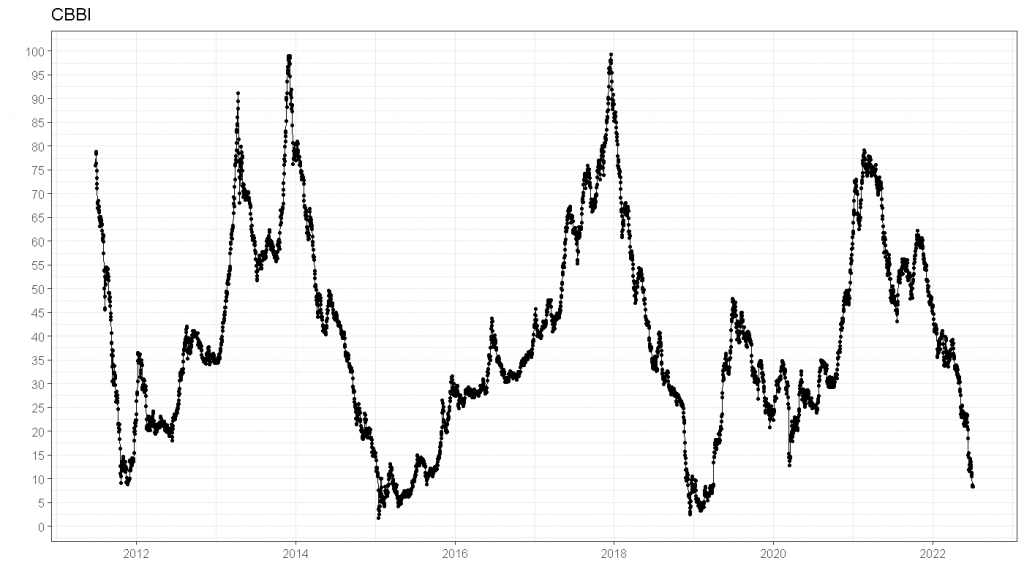
ggplot(cbbi, aes(x = Date, y = Price, color = Confidence)) +
geom_line(size = 3) +
geom_point(size = 3) +
theme_classic(base_size = 15) +
scale_y_log10(breaks = c(10, 100, 1000, 10000)) +
scale_color_viridis_c() +
ggtitle("Bitcoin 2011-07 - today", "Log-Scale")Code-Sprache: JavaScript (javascript)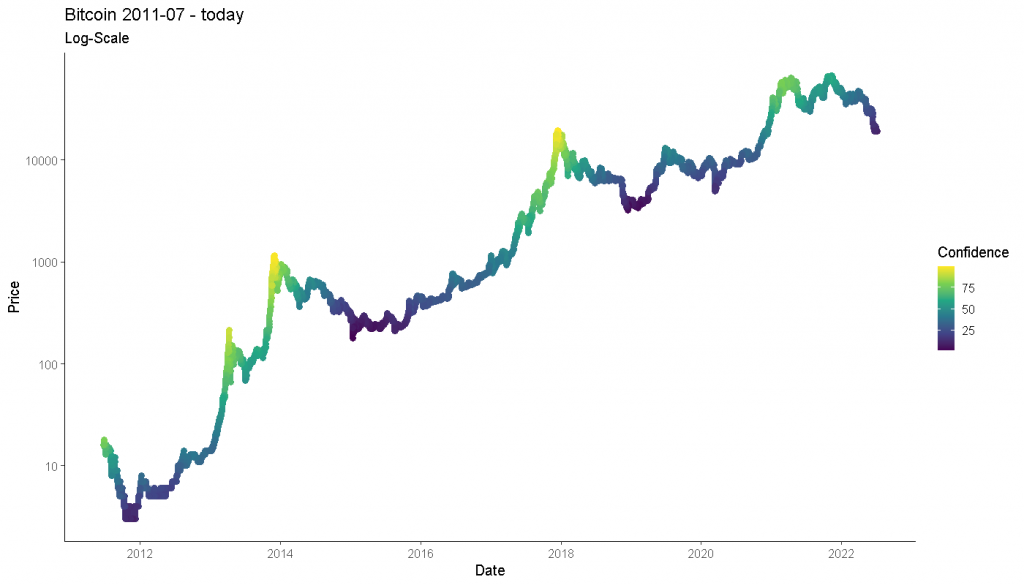
Lags von CBBI und Bitcoin-Preis erstellen
Nun erstellen wir eine Reihe ausgewälter Lags unterschiedlicher Länge (d.h. frühere Werte) 1,5, …, 2200 für den CBBI. Um dann die Korrelation zwischen bestimmten CBBI-Werten in der Vergangenheit und dem Bitcoin-Preis zu untersuchen, erstellen wir identische Lags für den Bitcoin-Preis, die jedoch um einen Tag in die Zukunft verschoben werden. So können wir beispielsweise den CBBI-Wert von gestern mit dem heutigen Bitcoin-Preis in Beziehung setzen.
Natürlich möchten wir das Gleiche nicht nur für einen Tag, sondern auch für längere Zeiträume tun, daher die Lags bis zu 2200 Tagen. Zum Beispiel ist cbbi_300 der Wert des CBBI vor 300 Tagen, und btc_return_300 ist die Bitcoin-Rendite in den 300 folgenden Tagen. Auf diese Weise können wir immer übereinstimmende Zeiträume in Beziehung setzen.
cbbi <- cbbi %>%
arrange(Date) %>%
mutate(
cbbi_1 = dplyr::lag(Confidence, 1),
cbbi_5 = dplyr::lag(Confidence, 5),
cbbi_10 = dplyr::lag(Confidence, 10),
cbbi_20 = dplyr::lag(Confidence, 20),
cbbi_40 = dplyr::lag(Confidence, 40),
cbbi_150 = dplyr::lag(Confidence, 150),
cbbi_300 = dplyr::lag(Confidence, 300),
cbbi_600 = dplyr::lag(Confidence, 600),
cbbi_1400 = dplyr::lag(Confidence, 1400),
cbbi_2200 = dplyr::lag(Confidence, 2200)
) %>%
rename(fg = Confidence)
# Create BTC returns
cbbi <- cbbi %>%
mutate(
btc_return_1 = lead(Price) / Price - 1,
btc_return_5 = lead(Price) / lag(Price, 4) - 1,
btc_return_10 = lead(Price) / lag(Price, 9) - 1,
btc_return_20 = lead(Price) / lag(Price, 19) - 1,
btc_return_40 = lead(Price) / lag(Price, 39) - 1,
btc_return_150 = lead(Price) / lag(Price, 150) - 1,
btc_return_300 = lead(Price) / lag(Price, 299) - 1,
btc_return_600 = lead(Price) / lag(Price, 599) - 1,
btc_return_1400 = lead(Price) / lag(Price, 1399) - 1,
btc_return_2200 = lead(Price) / lag(Price, 2199) - 1
)Code-Sprache: PHP (php)Streudiagramme des Bitcoin Fear and Greed Index vs. Bitcoin Preis
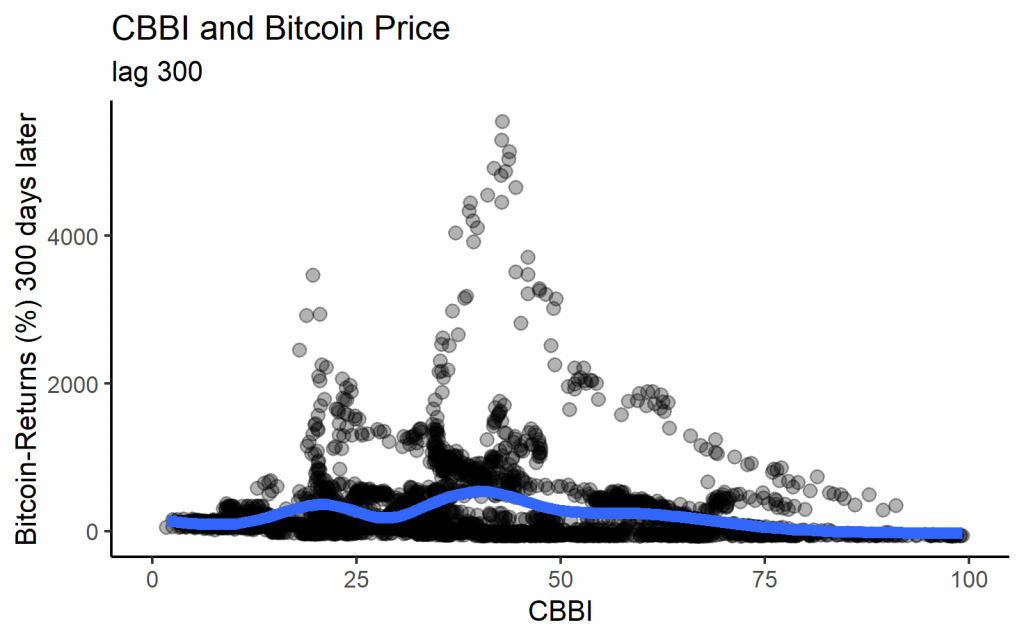
Die folgenden Diagramme erhalten wir, wenn wir den vergangenen Wert des CBBI mit der entsprechenden Bitcoin-Rendite für jeden Tag als Streudiagramm darstellen. Betrachtet man verschiedene Lags, so ergeben sich recht unterschiedliche Muster. Bei geringeren Lags wurden die höchsten Bitcoin-Renditen in der Regel durch mittlere CBBI-Werte angezeigt. Fast alle der extrem hohen Renditen stammen jedoch aus dem Jahr 2013. Bei langen Lags sehen wir tatsächlich das erwartete Muster, dass niedrige CBBI-Werte zu hohen Renditen führen, während hohe CBBI-Werte niedrigen Renditen vorausgehen.
Die Tatsache, dass nur lange Verzögerungen die erwartete Korrelation mit dem Bitcoin-Kurs aufweisen, steht im Einklang mit dem Ziel des CBBI, einen „Makro“-Indikator zu liefern, der die langfristigeren Höchst- und Tiefststände identifiziert.
Der Lag von 1400 Tagen ist für solch einen Zyklus-Indikator intuitiv, da die Verzögerung von 1400 Tagen in etwa der Zeit zwischen den letzten Bitcoin-Halbierungen entspricht, was als Schätzung für die Länge des „inhärenten“ Bitcoin-Zyklus dienen könnte.
ggplot(cbbi %>%
mutate(btc_return_20 = btc_return_20 * 100),
aes(x = cbbi_20, y = btc_return_20)) +
geom_point(size = 3, alpha = 0.3) +
geom_smooth(size = 3, se = FALSE) +
theme_classic(base_size = 15) +
xlim(0, 100) +
xlab("CBBI") +
ylab("Bitcoin-Returns (%) 20 days later") +
ggtitle("CBBI and Bitcoin Price", "lag 20")
ggplot(cbbi %>%
mutate(btc_return_300 = btc_return_300 * 100),
aes(x = cbbi_300, y = btc_return_300)) +
geom_point(size = 3, alpha = 0.3) +
geom_smooth(size = 3, se = FALSE) +
theme_classic(base_size = 15) +
xlim(0, 100) +
xlab("CBBI") +
ylab("Bitcoin-Returns (%) 300 days later") +
ggtitle("CBBI and Bitcoin Price", "lag 300")
ggplot(cbbi %>%
mutate(btc_return_1400 = btc_return_1400 * 100),
aes(x = cbbi_1400, y = btc_return_1400)) +
geom_point(size = 3, alpha = 0.3) +
geom_smooth(size = 3, se = FALSE) +
theme_classic(base_size = 15) +
xlim(0, 100) +
xlab("CBBI") +
ylab("Bitcoin-Returns (%) 1400 days later") +
ggtitle("CBBI and Bitcoin Price", "lag 1400")Code-Sprache: PHP (php)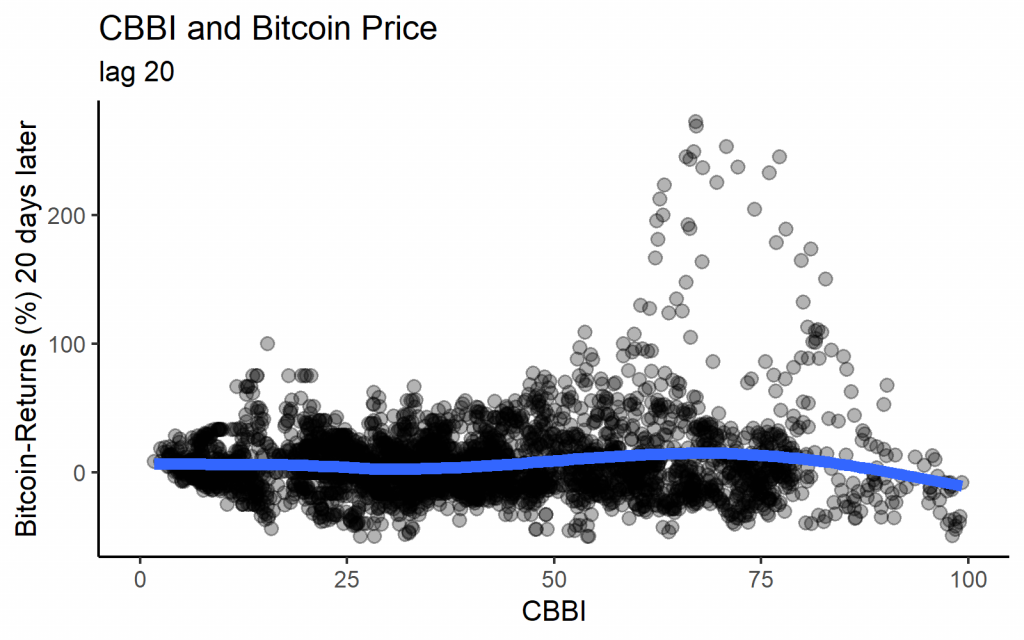
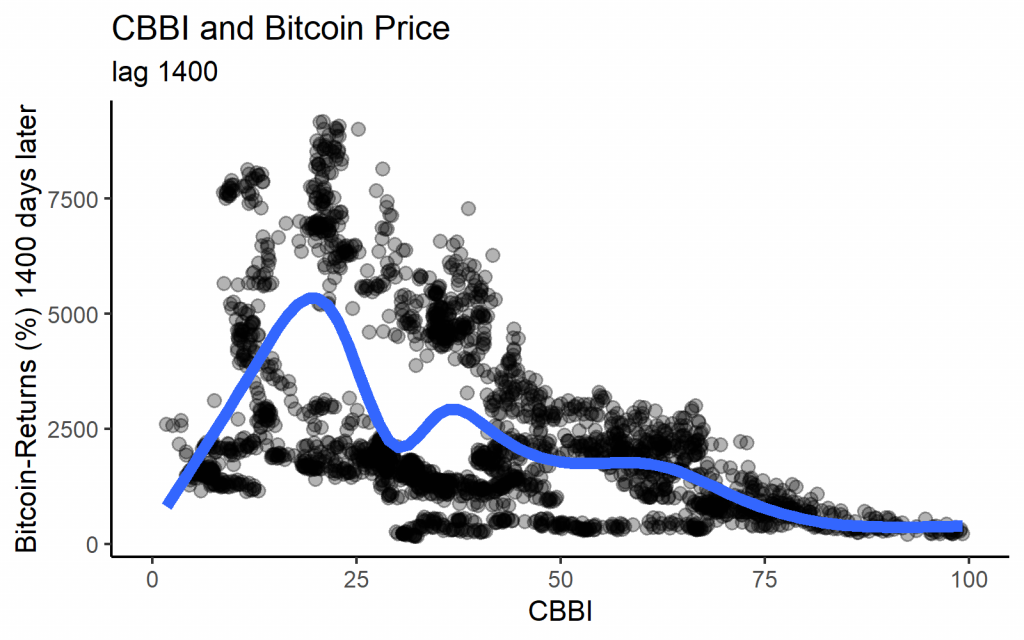
Wie stabil ist die Beziehung zwischen dem CBBI und dem Bitcoin-Kurs?
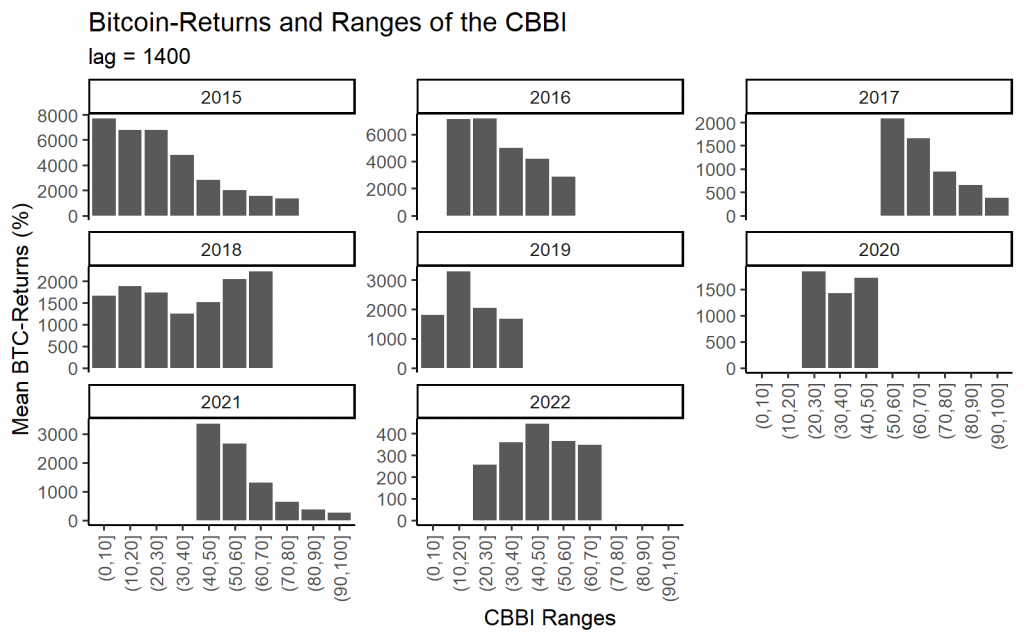
Ein weiteres hilfreiches Diagramm zur Veranschaulichung des Zusammenhangs zwischen dem CBBI und dem Bitcoin-Kurs ist der Binned Barplot. Er zeigt die durchschnittliche Bitcoin-Rendite in Abhängigkeit von der Bandbreite der CBBI-Werte. Auch hier ist die Korrelation zwischen dem CBBI und dem Bitcoin-Kurs bei relativ langen Verzögerungen von 150 oder 1400 Tagen negativ.

Wenn man die Daten in einzelne Jahre aufteilt, wird die Beziehung stärker verrauscht, aber in den meisten Jahren ist immer noch eine negative Beziehung erkennbar.
cbbi_150_bins <- cbbi %>%
mutate(cbbi_150_bin = cut(x = cbbi_150, breaks = seq(from = 0, to = 100, by = 10))) %>%
group_by(cbbi_150_bin) %>%
summarise(mean_ret = mean(btc_return_150, na.rm = T)) %>%
mutate(mean_ret = mean_ret * 100) %>%
ungroup %>%
drop_na()
ggplot(cbbi_150_bins, aes(x = cbbi_150_bin, y = mean_ret)) +
geom_bar(stat = "identity") +
xlab("CBBI Index Ranges") +
ylab("Mean BTC-Returns (%)") +
ggtitle("BTC-Returns and Ranges of the CBBI", "lag = 150") +
theme_classic(base_size = 10)
cbbi_1400_bins <- cbbi %>%
mutate(year = year(Date)) %>%
mutate(cbbi_1400_bin = cut(x = cbbi_1400, breaks = seq(from = 0, to = 100, by = 10))) %>%
group_by(cbbi_1400_bin, year) %>%
summarise(mean_ret = mean(btc_return_1400, na.rm = T)) %>%
mutate(mean_ret = mean_ret * 100) %>%
ungroup %>%
drop_na()
ggplot(cbbi_1400_bins, aes(x = cbbi_1400_bin, y = mean_ret)) +
geom_bar(stat = "identity") +
xlab("CBBI Ranges") +
ylab("Mean BTC-Returns (%)") +
ggtitle("Bitcoin-Returns and Ranges of the CBBI", "lag = 1400") +
theme_classic(base_size = 10) +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1)) +
facet_wrap(~year, scales = "free_y")Code-Sprache: JavaScript (javascript)Backtest des Bitcoin Fear and Greed Index
Lineare Strategie
Bevor wir zu realistischeren Simulationen übergehen, ist es eine gute Idee, den vermuteten Effekt so isoliert wie möglich zu testen. Zu diesem Zweck entwickeln wir eine lineare Strategie, bei der die Bitcoin-Position linear (im Sinne einer linearen Funktion) von den CBBI-Werten abhängt. Die Positionsgröße sollte bei niedrigen CBBI-Werten am größten und bei hohen CBBI-Werten am kleinsten sein. Schließlich legt die negative Beziehung zwischen CBBI-Werten und Bitcoin-Renditen nahe, dass es vorteilhaft wäre, Bitcoin zu kaufen, wenn der Index niedrig ist und umgekehrt. Kurz gesagt, wir verwenden die folgende Formel:
Größe = (100 – CBBI) / 100
Sizing der „linearen“ Strategie
Unsere Positionsgröße bewegt sich also automatisch zwischen 0 und 1. Null würde bedeuten, dass wir 100 % Bargeld halten, und 1 würde bedeuten, dass wir 100 % Bitcoin halten.
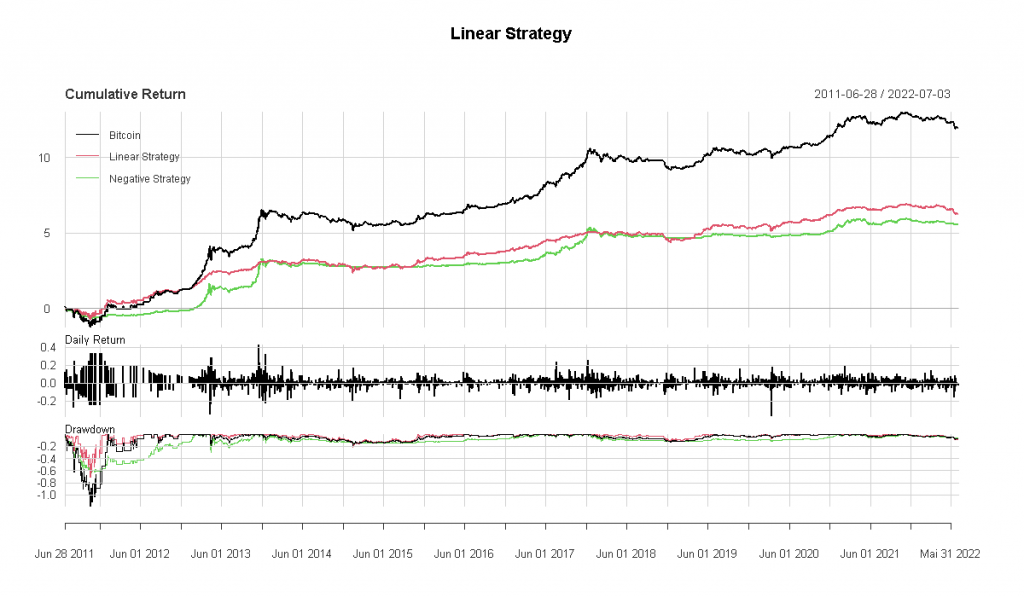
So sähe das Kapitalwachstum aus, wenn diese lineare Strategie umgesetzt würde. Die Transaktionskosten werden hier nicht berücksichtigt, aber es geht darum, den Effekt isoliert zu betrachten, bevor wir einen realistischeren Test durchführen.
library(xts)
library(PerformanceAnalytics)
cbbi <- cbbi %>%
ungroup() %>%
mutate(Exposure = (100 - cbbi_1) / 100,
lin_size = Exposure)
ggplot(cbbi, aes(x = Date, y = lin_size)) +
geom_line()
ggplot(cbbi, aes(x = Date, y = Price, color = Exposure)) +
geom_line(size = 3) +
geom_point(size = 3) +
scale_color_viridis_c() +
theme_classic(base_size = 25) +
xlab("") +
ylab("Bitcoin") +
ggtitle("Linear Strategy") +
scale_y_log10()
dat_bt <- cbbi %>%
mutate(lin_strat_return = btc_return_1 * lin_size) %>%
mutate(lin_strat_rev_return = btc_return_1 * (-lin_size + 1)) %>%
select(Date, Price, lin_size, lin_strat_return, lin_strat_rev_return) %>%
drop_na() %>%
mutate(lin_strat_equity = cumprod(1 + lin_strat_return))
btc_ret <- cbbi %>%
mutate(btc_ret = Price / dplyr::lag(Price) - 1) %>%
select(Date, btc_ret) %>%
drop_na()
btc_ret_xts <- xts(btc_ret$btc_ret, order.by = btc_ret$Date)
strat_ret_xts <- xts(dat_bt$lin_strat_return, order.by = dat_bt$Date)
strat_ret_rev_xts <- xts(dat_bt$lin_strat_rev_return, order.by = dat_bt$Date)
bt_xts <- merge(btc_ret_xts, strat_ret_xts, strat_ret_rev_xts)
bt_xts <- na.omit(bt_xts)
colnames(bt_xts) <- c("Bitcoin", "Linear Strategy", "Negative Strategy")
charts.PerformanceSummary(bt_xts, geometric = F, main = "Linear Strategy")
table.AnnualizedReturns(bt_xts, geometric = F, scale = 365)Code-Sprache: JavaScript (javascript)Ehrlich gesagt gibt es hier leider (noch?) nicht viel zu sehen. Die auf dem CBBI basierende Strategie ist der negativen Variante derselben Strategie (Kauf bei hohen CBBI-Werten) nur geringfügig überlegen. Wie jedoch bereits erwähnt, ist der CBBI ein Makro-Indikator, und dieser Test basierte auf Lags von einem Tag, so dass wir vielleicht einen längeren Zeitrahmen in Betracht ziehen müssen.
Backtest mit festem Cutoff für den CBBI
In der Praxis würde man sicherlich nicht die lineare Strategie verfolgen, bei der man die Positionsgröße täglich anpassen müsste, sondern man würde vermutlich einen oder mehrere Grenzwerte wählen, über oder unter denen man Bitcoin halten würde.
Eine einfache Strategie könnte wie folgt aussehen:
- Kaufen, wenn der CBBI unter 10 liegt
- Verkaufen, wenn der CBBI über 90 liegt. Dann in Cash bleiben, bis der CBBI wieder unter 10 fällt.
Mit diesem Grenzwert wäre die Strategie etwa ein Viertel der Zeit vollständig in Cash gewesen. Vermutlich kommt diese Strategie der beabsichtigten Verwendung des CBBI sehr nahe. Die CBBI versucht, Blow-Off-Tops und längerfristige Tiefs zu erkennen; daher scheinen solche extremen Cutoffs geeignet.
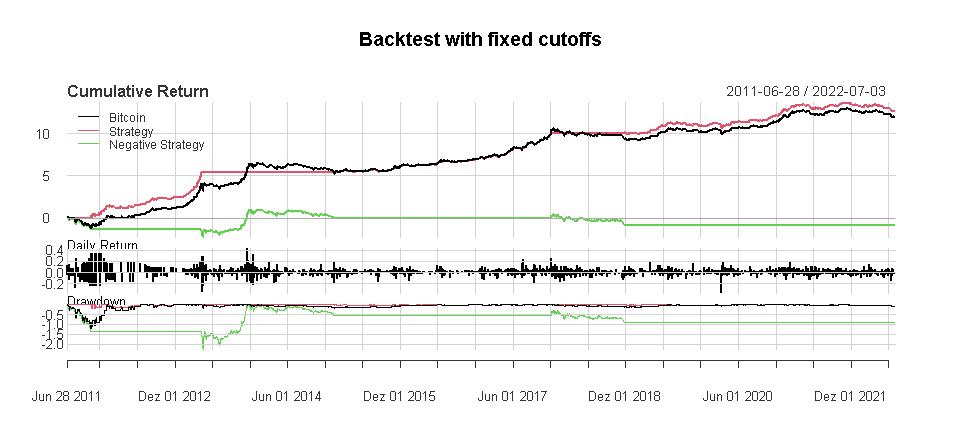
Leider waren die beiden Höchststände des Jahres 2021 keine „Blow-off“-Tops, und der CBBI konnte diese nicht erkennen. Mit einem oberen Cutoff von 70 sehen die Ergebnisse ansprechender aus, aber an dieser Stelle betreiben wir vermutlich schon Backfitting der Parameter zur Optimierung des Backtests für die Vergangenheit (Overfitting).
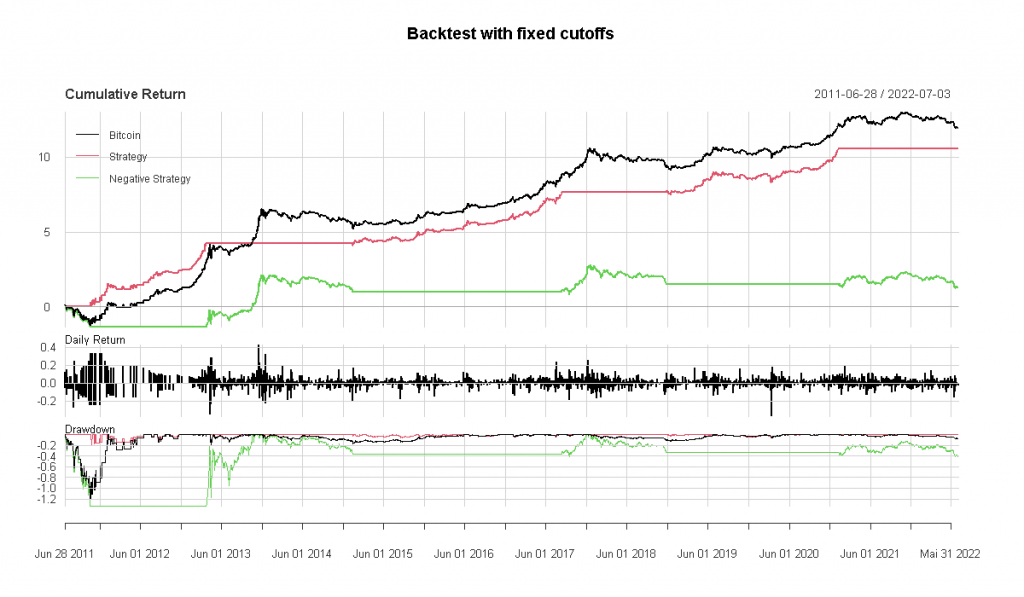
dat_bt <- cbbi
dat_bt$signal <- NA
cutoff_low <- 10
cutoff_high <- 100 - 30
dat_bt$signal <- 0
for (i in 2:(nrow(dat_bt))) {
if (dat_bt$fg[i] < cutoff_low) {
dat_bt$signal[i] <- 1
} else if (dat_bt$fg[i] > cutoff_high) {
dat_bt$signal[i] <- 0
} else {
dat_bt$signal[i] <- dat_bt$signal[i - 1]
}
}
dat_bt$signal[is.na(dat_bt$signal)] <- 0
dat_bt %>%
count(signal)
ggplot(dat_bt, aes(x = Date, y = signal)) +
geom_area()
dat_bt <- dat_bt %>%
ungroup() %>%
arrange(Date) %>%
mutate(cbbi_ret = ifelse(signal > 0.5, btc_return_1, 0)) %>%
mutate(cbbi_ret_reverse = ifelse(signal < 0.5, btc_return_1, 0)) %>%
select(Date, cbbi_ret, cbbi_ret_reverse) %>%
drop_na() %>%
mutate(cbbi_equity = cumprod(1 + cbbi_ret))
btc_ret <- cbbi %>%
mutate(btc_ret = Price / dplyr::lag(Price) - 1) %>%
select(Date, btc_ret) %>%
drop_na()
btc_ret_xts <- xts(btc_ret$btc_ret, order.by = btc_ret$Date)
strat_ret_xts <- xts(dat_bt$cbbi_ret, order.by = dat_bt$Date)
strat_ret_rev_xts <- xts(dat_bt$cbbi_ret_reverse, order.by = dat_bt$Date)
bt_xts <- merge(btc_ret_xts, strat_ret_xts, strat_ret_rev_xts)
bt_xts <- na.omit(bt_xts)
colnames(bt_xts) <- c("Bitcoin", "Strategy", "Negative Strategy")
charts.PerformanceSummary(bt_xts, geometric = F,
main = "Backtest with fixed cutoffs")
table.AnnualizedReturns(bt_xts, geometric = F)Code-Sprache: PHP (php)Im Allgemeinen stehen Indizes wie der CBBI vor der Herausforderung, dass sie nur auf eine sehr begrenzte Anzahl von Markthochs und -tiefs trainiert werden können. Im Fall von Bitcoin haben wir bisher nur zwei eindeutige Blow-off-Tops gesehen.
Der CBBI wurde mehrmals geändert, um das Wissen über Marktentwicklungen zu berücksichtigen. So wurde beispielsweise das Stock-to-Flow-Modell aus dem Index gestrichen. Ziel ist es, einen stabilen Satz von Teilindikatoren zu schaffen, die sich zur Identifizierung von Marktübertreibungen eignen, aber natürlich lässt sich nicht sagen, ob dieses Ziel jemals erreicht werden kann.
Da der CBBI kürzlich geändert wurde, beginnt der out-of-sample Zeitraum zur Beurteilung der Vorhersagekraft des Index ehrlicherweise erst jetzt (erneut). Abschließend möchten wir noch den Autor des CBBI dafür loben, dass er durch die Freigabe des Codes und der Daten sehr transparent ist, was längst nicht für alle Sentiment-Indikatoren gilt.




